Самая простая нейронная сеть на Python

Мы сейчас переживаем настоящий бум нейронных сетей. Их применяют для распознания, локализации и обработки изображений. Нейронные сети уже сейчас умеют многое что не доступно человеку. Нужно же и самим вклиниваться в это дело! Рассмотрим нейтронную сеть которая будет распознавать числа на входном изображении. Все очень просто: всего один слой и функция активации. Это не позволит нам распознать абсолютно все тестовые изображения, но мы справимся с подавляющим большинством. В качестве данных будем использовать известную в мире распознания чисел подборку данных MNIST.

Для работы с ней в Python есть библиотека python-mnist. Что-бы установить:

pip install python-mnist

Теперь можем загрузить данные

from mnist import MNIST
mndata = MNIST("/path_to_mnist_data_folder/")
tr_images, tr_labels = mndata.load_training()
test_images, test_labels = mndata.load_testing()

Архивы с данными нужно загрузить самостоятельно, а программе указать путь к каталогу с ними. Теперь переменные tr_images и test_images содержат изображения для тренировки сети и тестирования соотвественно. А переменные tr_labels и test_labels — метки с правильной классификацией (т.е. цифры с изображений). Все изображения имеют размер 28х28. Зададим переменную с размером.

img_shape = (28, 28)

Преобразуем все данные в массивы numpy и нормализуем их (приведем к размеру от -1 до 1). Это увеличит точность вычислений.

import numpy as np

for i in range(0, len(test_images)):
    test_images[i] = np.array(test_images[i]) / 255
    
for i in range(0, len(tr_images)):
    tr_images[i] = np.array(tr_images[i]) / 255

Отмечу, что хоть и изображения принято представлять в виде двумерного массива мы будем использовать одномерный, это проще для вычислений. Теперь нужно понять «что же такое нейронная сеть»! А это просто уравнение с большим количеством коэффициентов. Мы имеем на входе массив из 28*28=784 элементов и еще по 784 веса для определения каждой цифры. В процессе работы нейронной сети нужно перемножить значения входов на веса. Сложить полученные данные и добавить смещение. Полученный результат подать на функцию активации. В нашем случае это будет Relu. Эта функция равна нулю для всех отрицательных аргументов и аргументу для всех положительных.

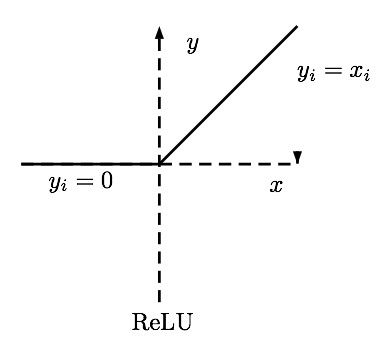
Есть еще много функций активации! Но это же самая простая нейронная сеть! Определим эту функцию при помощи numpy

def relu(x):
    return np.maximum(x, 0) 

Теперь чтобы вычислить изображение на картинке нужно просчитать результат для 10 наборов коэффициентов.

def nn_calculate(img):
    resp = list(range(0, 10))
    for i in range(0,10):
        r = w[:, i] * img
        r = relu(np.sum(r) + b[i])
        resp[i] = r

    return np.argmax(resp)

Для каждого набора мы получим выходной результат. Выход с наибольшим результатом вероятнее всего и есть наше число.

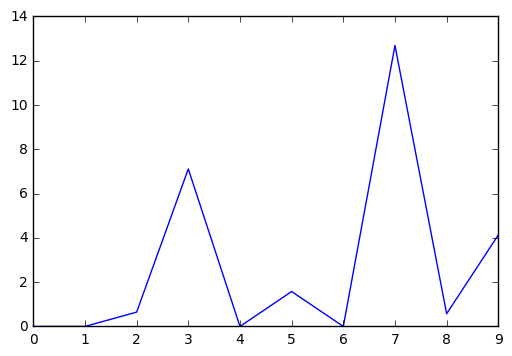
В данном случае 7. Вот и все! Но нет… Ведь нужно эти самые коэффициенты где-то взять. Нужно обучить нашу нейронную сеть. Для этого применяют метод обратного распространения ошибки. Его суть в том чтобы рассчитать выходы сети, сравнить их с правильными, а затем отнять от коэффициентов числа необходимые чтобы результат был правильным. Нужно помнить, что для того чтобы вычислить эти значения нужна производная функции активации. В нашем случае она равна нулю для всех отрицательных чисел и 1 для всех положительных. Определим коэффициенты случайным образом.

w = (2*np.random.rand(10, 784) - 1) / 10
b = (2*np.random.rand(10) - 1) / 10

for n in range(len(tr_images)):
    img = tr_images[n]
    cls = tr_labels[n]
    #forward propagation 
    resp = np.zeros(10, dtype=np.float32)
    for i in range(0,10):
        r = w[i] * img
        r = relu(np.sum(r) + b[i])
        resp[i] = r

    resp_cls = np.argmax(resp)
    resp = np.zeros(10, dtype=np.float32)
    resp[resp_cls] = 1.0

    #back propagation
    true_resp = np.zeros(10, dtype=np.float32)
    true_resp[cls] = 1.0

    error = resp - true_resp

    delta = error * ((resp >= 0) * np.ones(10))
    for i in range(0,10):
        w[i] -= np.dot(img, delta[i])
        b[i] -= delta[i]

В процессе обучения коэффициенты станут слегка похожи на числа:

Проверим точность работы:

def nn_calculate(img):
    resp = list(range(0, 10))
    for i in range(0,10):
        r = w[i] * img
        r = np.maximum(np.sum(r) + b[i], 0) #relu
        resp[i] = r

    return np.argmax(resp)

total = len(test_images)
valid = 0
invalid = []

for i in range(0, total):
    img = test_images[i]
    predicted = nn_calculate(img)
    true = test_labels[i]
    if predicted == true:
        valid = valid + 1
    else:
        invalid.append({"image":img, "predicted":predicted, "true":true})

print("accuracy {}".format(valid/total))

У меня получилось 88%. Не так уж круто, но очень интересно!