В наше время уже невозможно представить мир без цифровой электроники. Каждый из нас имеет персональный компьютер, телефон и ещё кучу устройств, работа которых невозможна без цифровых сигналов. Но и без аналогового мира не обойтись. Мы постоянно должны учитывать температуру, влажность окружающей среди и ещё кучу аналоговых величин. Следовательно приходится преобразовывать аналоговые сигналы в цифровые и назад.
Процесс преобразования аналогового сигнала в цифровой тесно связан с квантованием сигнала по уровню и времени.
И тут к нам на помощь приходит теорема Котельникова (для безошибочного преобразования следует выбрать частоту дискретизации в 2 раза больше частоты наивысшей гармоники спектра). Теперь на пальцах.
Имеет сигнал:
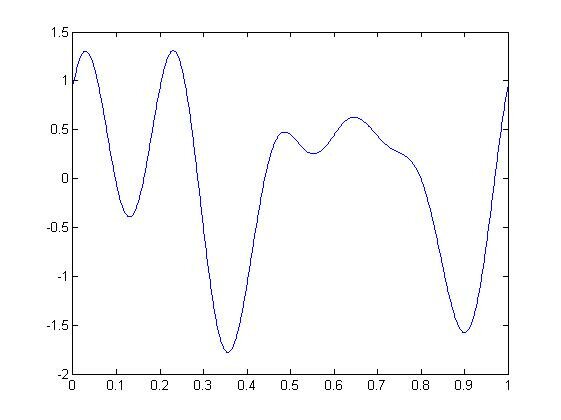
Который представляет собой сумму трёх синусоид с амплитудами 0.8, 0.7 и 0.5 частотой 2, 4 и 5 ну и сдвигом по фазе 0, 90, 30 градусов.
Из сего видим что наивысшей частотой является — 5.
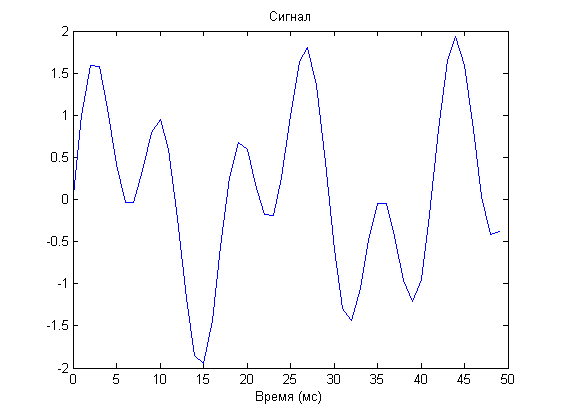
Применим теорему Котельникова и найдём частоту Котельникова (Найквиста): 10 Т.е. при дискретизации с частотой выше этой мы можем безошибочно восстановить исходный сигнал. При квантовании с частотой 0.8 частоты Котельникова имеем:
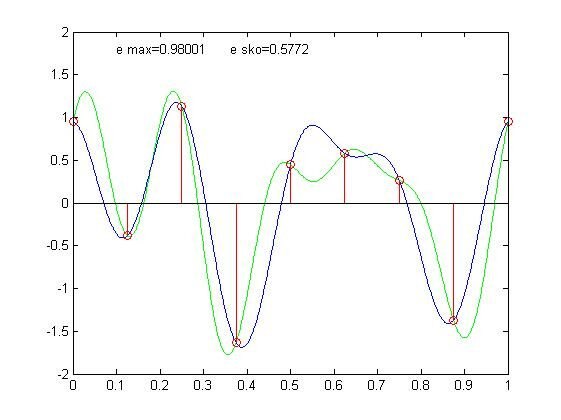
Не вооруженным взглядом видно наличие искажений (синий — исходный сигнал, зелёный — восстановлены в соответствии с теоремой Котельникова).
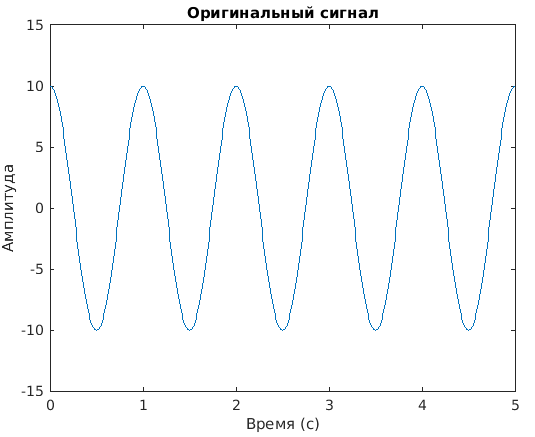
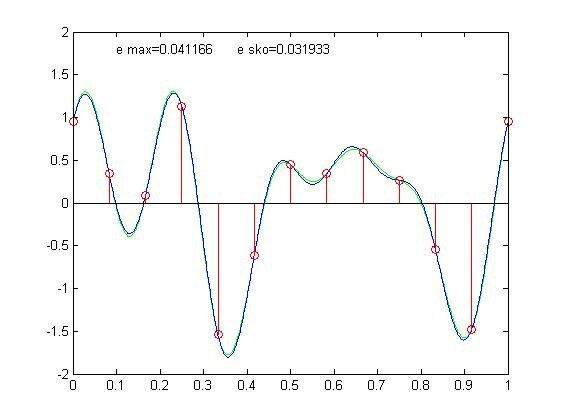
При квантовании с частотой больше 10 искажений при восстановлении не наблюдается:
Вот и вся наука на сегодня.