Рассмотрим процесс фильтрации сигнала при помощи цифрового фильтра в Matlab.
Открываем матлаб и начинаем выполнять функции.
Сначала зададим параметры.
Fs=100; % частота дискретизации tmax=5; % промежуток рассматриваемого времени Nsamps = tmax*Fs; % рассматриваемый период
Задаём временную шкалу для нашего сигнала:
t = 1/Fs:1/Fs:tmax;
Теперь задаём сигнал и помеху:
s1 = 10*cos(2*pi*t); % сигнал s2 = 2*cos(20*pi*t + pi/4); % высокочастотная помеха s3 = s1 + s2; % всё вместе
Выведем на экран сигналы.
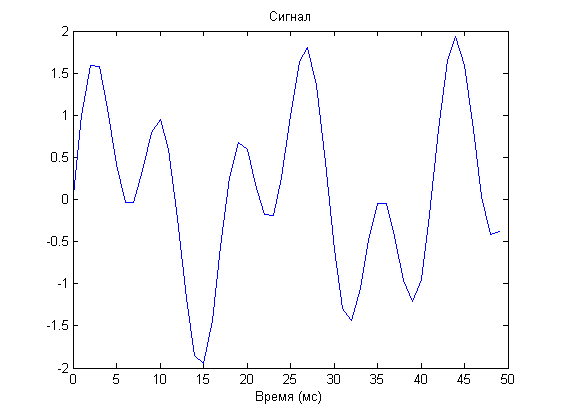
Оригинальный сигнал:
plot(t,s1)
ylabel('Амплитуда')
xlabel('Время (с)')
title('Оригинальный сигнал')
ylim([-15 15])
Вот что получилось:
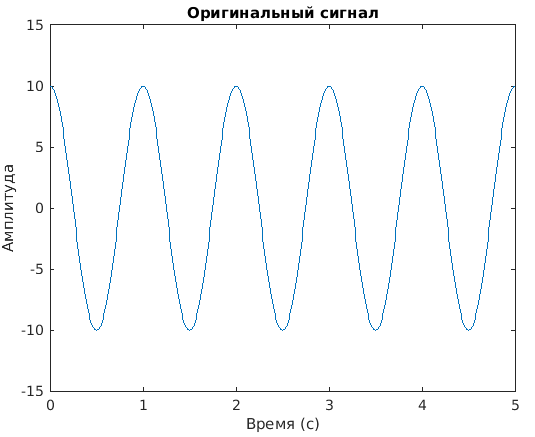
Теперь сигнал с высокочастотной помехой:
figure
plot(t,s3)
xlabel('Время (с)')
ylabel('Амплитуда')
title('Сигнал с помехой')ylim([-15 15])
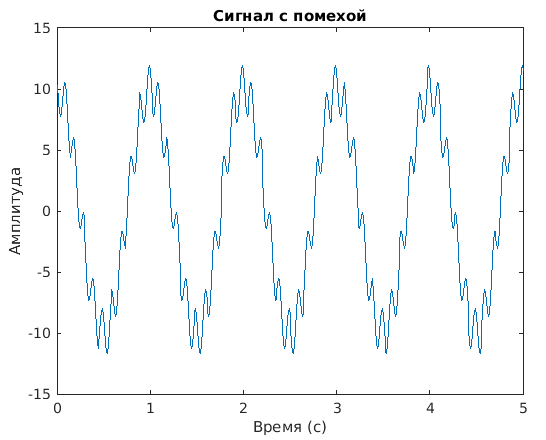
Синтезировать мы фильтр сегодня не будем, а воспользуемся простейшим случаем БИХ фильтра нижних частот.
Задаём коэффициенты фильтра:
b = 1; a = [1 -1];
Фильтруем сигнал при помощи функции filter :
s3_f = filter(b,a,s3);
Теперь нужно изменить амплитуду результата. Если честно понятия не имею почему она в 15 раз больше чем нужно:
s3_f = s3_f/15;
Выводим результат:
figure
plot(t,s3_f)
xlabel('Время (с)')
ylabel('Амплитуда (В)')
title('Сигнал после фильтрации')
ylim([-15 15])
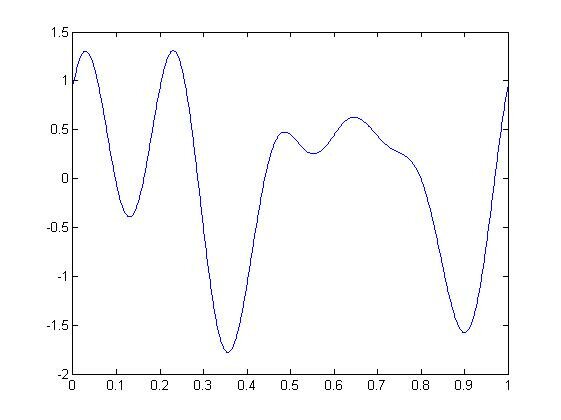
Результат выполнения должен быть таким:
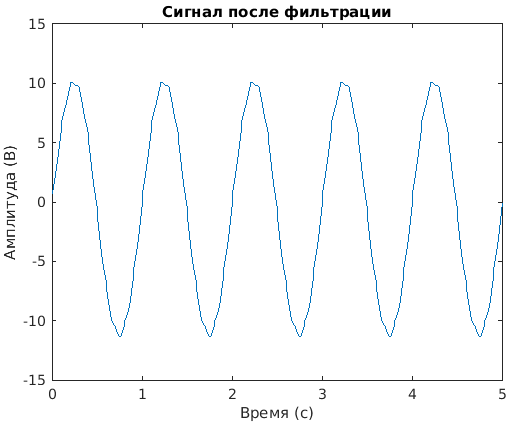
В ближайшее время будет ещё статья о разборе спектра сигнала.