Фильтры с конечной импульсной характеристикой имеют структурную форму вида:
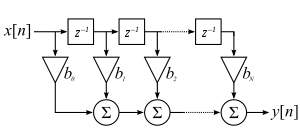
В силу своего строения они всегда устойчивы, что безусловно является плюсом, но содержат больше звеньев по сравнению с аналогичными фильтрами с бесконечной импульсной характеристикой.
Приступим к синтезу и анализу характеристик КИХ фильтра в пакете matlab.
Будем синтезировать фильтр нижних частот с частотой среза 0.2 (частота относительно частоты дискретизации).
Отметим, что вследствии преобразований необходимых для вычислений в матлаб необходимо частоту среза задать вдвое большей от необходимой нам относительной частоты.
Зададим начальные условия:
>> clear, N=26; fc1=0.4;
Где N — количество звеньев в фильтре. Воспользуемся оконным методом синтеза с прямоугольным окном.
>> win = boxcar(N);
Теперь можно синтезировать КИХ фильтр нижних частот:
>> h = fir1(N-1,fc1,win,'noscale')
График импульсной характеристики можно вывести так:
>> stem(h)
У нас он имеет вид:
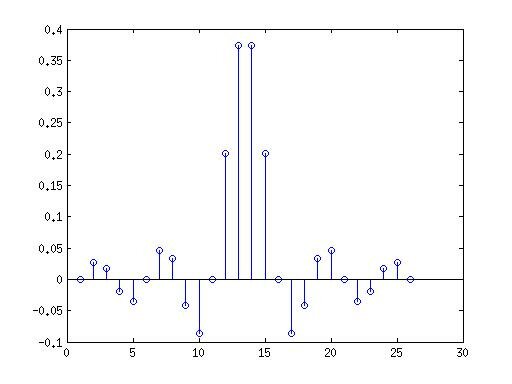
Сформируем сетки частот для вычисления частотных характеристик:
>> f = [0:0.005:0.5];w=2*pi*f;
Для вычисления частотных характеристик будем считать полином знаменателя еденицой:
>> b=1;
Частотную характеристуку вычисляем так:
>> H=freqz(h,b,w);
Теперь вычисляем АЧХ фильтра и выводим его на экран:
>> HA=abs(H); >> plot(f,HA),axis([0 0.5 -0.05 1.15]), grid on
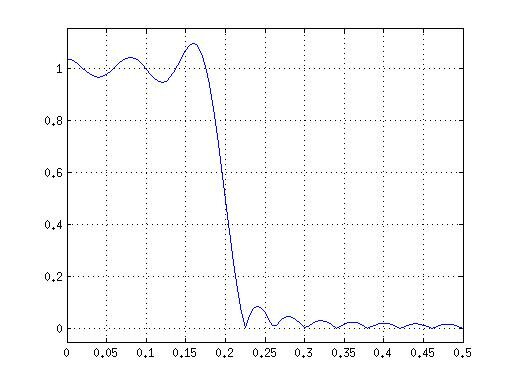
Как видите полученный фильтр соответствует заданным параметрам, т.е. поставленная задача выполнена. Вы можете наблюдать на графике АЧХ явление Гиббса (пульсации).
Был синтезирован простой фильтр, с простейшим из всех окон.